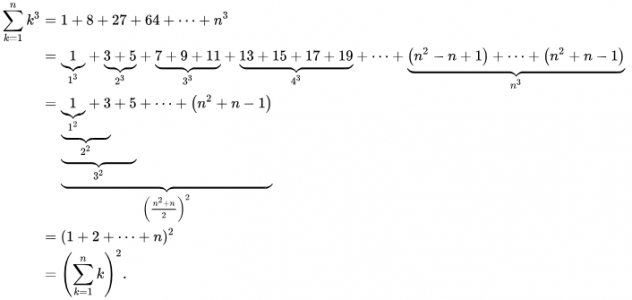En complément de la vidéo de l'épisode n°27 sur les nombres impairs, voici la manière dont Boèce présente la propriété 1=1², 1+3=2², 1+3+5=3² et ainsi de suite :
"Parmi ces nombres, si je considère 1, je vois naître le premier carré en puissance. Mais si à 1 j'ajoute le troisième, en laissant celui qui le précède, j'obtiens le second carré : car si, laissant 2, j'ajoute 3 à l, je fais naître 4, qui est un carré. Si maintenant, laissant le nombre médian, 4, j'ajoute de la même façon à 1 et 3 le nombre 5, je vois naître le troisième carré, 9 : car 1 et 3 et 5 font 9. Mais si, laissant dans l'intervalle le nombre 6, j'ajoute 7 aux nombres précédents, le total monte à 16, c'est-à-dire à la valeur du quatrième carré. Résumons clairement la manière de faire naître cette sorte de nombre : si l'on additionne entre eux tous les impairs, suivant la série du nombre naturel évidemment, on obtient le tissu des carrés."
Institution arithmétique, II, 12
Et voici la manière dont on démontre l'égalité énoncée en fin de vidéo sur la somme des n premiers cubes :
Image :
|
Dans la même chronique
Arithm’Antique n°66 – Lewis Carroll et le « No Election »
Arithm’Antique n°65 – La méthode de Condorcet contre les cycles
Dernières chroniques
De(s) Contractions – Saison 7 Semaine 6
