Arithm'Antique - Bonus n°25 : L'Arbêlos

Tous les jeudis, Antoine Houlou-Garcia vous fait aimer les mathématiques à travers la philosophie, l'art, la mytholgie et l'histoire !

Le Livre des lemmes, qui ne nous est parvenu qu’en latin et qui compile quelques résultats sans doute trouvés par Archimède, s’intéresse à une forme particulière : l’arbêlos. Ce terme désigne à l’origine le couteau du cordonnier dont la lame ressemble à l’aire qui intéresse le génie de Syracuse. Voici la démonstration d'Archimède telle qu'évoquée dans la vidéo n°25 d'Arithm'Antique. 

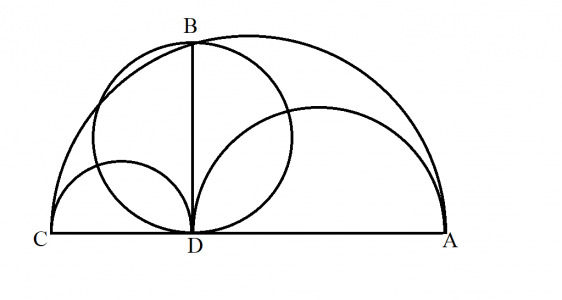
Soit ABC un demi-cercle ; construisons sur le diamètre AC deux demi-cercles (sc. tangents entre eux), l’un (sc. sur) AD, l’autre (sc. sur) DC, et élevons la perpendiculaire DB (sc. à CA) ; la figure ainsi déterminée, appelée arbêlos par Archimède (c’est-à-dire l’aire comprise entre l’arc du grand demi-cercle et les circonférences des deux petits demi-cercles) est équivalente au cercle ayant pour diamètre la perpendiculaire DB.  

Démonstration. Puisque DB est la moyenne proportionnelle^[1] entre DA et DC, le rectangle de côtés AD et DC sera équivalent au carré sur DB. Ajoutons de part et d’autre le rectangle de côtés AD et DC et les deux carrés AD sur DC ; le double du rectangle de côtés AD et DC, augmenté des deux carrés sur AD et sur DC, c’est-à-dire le carré sur AC, sera alors équivalent au double du carré sur DB, augmenté des deux carrés sur AD et sur DC. Or le rapport des cercles est égal au rapport des carrés (sc. sur leurs diamètres) ; il s’ensuit que le cercle de diamètre AC est équivalent à la somme du double du cercle de diamètre DB et des deux cercles de diamètres AD et, DC, et que le demi-cercle de diamètre AC est équivalent à la somme du cercle de diamètre DB et des deux demi-cercles de diamètres AD et DC. Retranchons de part et d’autre les deux demi-cercles de diamètres AD et DC. La figure qui reste d’un côté, à savoir l’aire comprise entre les demi-cercles sur AC, AD et DC (et c’est là la figure appelée arbêlos par Archimède), est alors équivalente (sc. à la figure qui reste de l’autre côté, à savoir) au cercle de diamètre DB, et c’est ce que nous avons voulu démontrer.

Le livre des lemmes, 4