Arithm’Antique - Bonus n°10

Compléments à l’épisode 10

Pour compléter la vidéo consacrée à l’infini, voici le moment dans La Docte ignorance où Nicolas de Cues expose comment le passage à l’infini crée nécessairement un changement de concept avec la très belle image du cercle qui devient une droite :

« Je déclare donc que, s'il y avait une ligne infinie, elle serait une droite, un triangle, un cercle, une sphère. Et, de même, s'il y avait une sphère infinie, elle serait un cercle, un triangle et une ligne. Et il faut dire la même chose du triangle infini et du cercle infini.

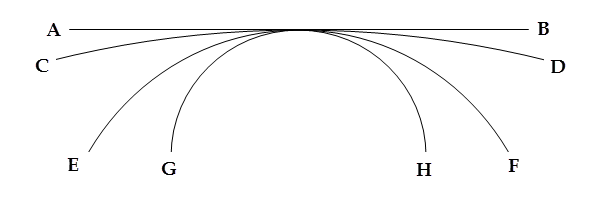
Premièrement, il est évident qu'une ligne infinie est une droite. Le diamètre d'un cercle est une ligne droite, et la circonférence est une ligne courbe plus grande que le diamètre. Si donc la ligne courbe est d'autant moins courbe que la circonférence est celle d'un cercle d'autant plus grand, alors la circonférence du cercle maximum, qui ne peut être plus grande, est courbe au minimum et droite au maximum. Ainsi, le maximum coïncide avec le minimum, et l'œil voit qu'il est nécessaire dans ces conditions que la ligne maximale soit courbe au minimum et droite au maximum.

Et sur ce point, il ne peut rester le moindre doute quand on voit, sur la figure ci-contre, comment l'arc CD d'un plus grand cercle s'éloigne plus de la curvité que l'arc EF d'un cercle moins grand, et l'arc EF s'éloigne encore plus de la curvité que l'arc GH d'un cercle encore moins grand. Donc, la ligne droite AB sera l'arc du cercle maximum, qui ne peut être plus grand. »[1]

Image :

Quant à la phrase d’Anaxagore qui rappelle le fameux « Rien ne se perd, rien ne se crée : tout se transforme » attribué à Lavoisier, la voici citée par Hippocrate :

« Assurément, aucune des choses n’est détruite et nulle n’est engendrée, parce que rien encore n’existait auparavant ; en fait il se produit une altération par mélange et discrimination. »^[2]

En route vers l’épisode 11 !

Image :

Selon Philolaos, « la géométrie est le principe et la patrie de toutes les sciences »[3], c’est pourquoi les deux prochains épisodes seront consacrés aux constructions géométriques telles que les Grecs les aimaient : à la règle et au compas.

S’il est vrai que « a donné à la philosophie géométrique la forme d’une culture libérale, en reprenant les choses au commencement pour découvrir les principes, par un examen des théorèmes mettant en œuvre une méthode non empirique et purement intellectuelle ; c’est lui précisément qui découvrit la théorie des proportions et l’existence d’une structure des formes de l’univers »[4], c’est vers un adversaire de Socrate que nous tournerons peu à peu notre regard…